El aspecto más importante del trabajo de Maxwell en el electromagnetismo es el término que introdujo en la ley de Ampère; la derivada temporal de un campo eléctrico, conocido como corriente de desplazamiento. El trabajo que Maxwell publicó en 1865, A Dynamical Theory of the Electromagnetic Field, modificaba la versión de la ley de Ampère con lo que se predecía la existencia de ondas electromagnéticas propagándose, dependiendo del medio material, a la velocidad de la luz en dicho medio. De esta forma Maxwell identificó la luz como una onda electromagnética, unificando así la óptica con el electromagnetismo.2
Exceptuando la modificación a la ley de Ampère, ninguna de las otras ecuaciones era original. Lo que hizo Maxwell fue reobtener dichas ecuaciones a partir de modelos mecánicos e hidrodinámicos usando su modelo de vórtices de líneas de fuerza de Faraday.
En 1884, Oliver Heaviside junto con Willard Gibbs agrupó estas ecuaciones y las reformuló en la notación vectorial actual. Sin embargo, es importante conocer que al hacer eso, Heaviside usó derivadas parciales temporales, diferentes a las derivadas totales usadas por Maxwell, en la ecuación (54). Ello provocó que se perdiera el término vxBque aparecía en la ecuación posterior del trabajo de Maxwell (número 77). En la actualidad, este término se usa como complementario a estas ecuaciones y se conoce como fuerza de Lorentz.
La historia es aún confusa, debido a que el término ecuaciones de Maxwell se usa también para un conjunto de ocho ecuaciones en la publicación de Maxwell de 1865, A Dynamical Theory of the Electromagnetic Field, y esta confusión se debe a que seis de las ocho ecuaciones son escritas como tres ecuaciones para cada eje de coordenadas, así se puede uno confundir al encontrar veinte ecuaciones con veinte incógnitas. Los dos tipos de ecuaciones son casi equivalentes, a pesar del término eliminado por Heaviside en las actuales cuatro ecuaciones.
[editar]Detalle de las ecuaciones
[editar]Ley de Gauss
La ley de Gauss explica la relación entre el flujo del campo eléctrico y una superficie cerrada. Se define como flujo eléctrico ( ) a la cantidad defluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico (
) a la cantidad defluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico ( ) que pasa por una superficie.3 Matemáticamente se la expresa como:
) que pasa por una superficie.3 Matemáticamente se la expresa como:
 ) a la cantidad defluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico (
) a la cantidad defluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico ( ) que pasa por una superficie.3 Matemáticamente se la expresa como:
) que pasa por una superficie.3 Matemáticamente se la expresa como:La ley dice que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga (q) o la suma de las cargas que hay en el interior de la superficie y la permitividad eléctrica en el vacío (ε0), así:4 5
La forma diferencial de la ley de Gauss es
donde ρ es la densidad de carga. Esta expresión es para una carga en el vacío, para casos generales se debe introducir una cantidad llamadadensidad de flujo eléctrico ( ) y nuestra expresión obtiene la forma:
) y nuestra expresión obtiene la forma:
 ) y nuestra expresión obtiene la forma:
) y nuestra expresión obtiene la forma:[editar]Ley de Gauss para el campo magnético
Experimentalmente se llegó al resultado de que los campos magnéticos, a diferencia de los eléctricos, no comienzan y terminan en cargasdiferentes. Esta ley primordialmente indica que las líneas de los campos magnéticos deben ser cerradas. En otras palabras, se dice que sobre una superficie cerrada, sea cual sea ésta, no seremos capaces de encerrar una fuente o sumidero de campo, esto expresa la no existencia del monopolo magnético.6 Matemáticamente esto se expresa así:5
Su forma integral equivalente:
Como en la forma integral del campo eléctrico, esta ecuación sólo funciona si la integral está definida en una superficie cerrada.
[editar]Ley de Faraday-Lenz
La ley de Faraday nos habla sobre la inducción electromagnética, la que origina una fuerza electromotriz en un campo magnético. Es habitual llamarla ley de Faraday-Lenz en honor a Heinrich Lenzya que el signo menos proviene de la Ley de Lenz. También se le llama como ley de Faraday-Henry, debido a que Joseph Henry descubrió esta inducción de manera separada a Faraday pero casi simultáneamente.7 Lo primero que se debe introducir es la fuerza electromotriz (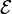 ), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:8
), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:8
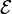 ), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:8
), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:8 ,
,
como el campo magnético es dependiente de la posición tenemos que el flujo magnético es igual a:
 .
.
Además, el que exista fuerza electromotriz indica que existe un campo eléctrico que se representa como:
con lo que finalmente se obtiene la expresión de la ley de Faraday:5
Lo que indica que un campo magnético que depende del tiempo implica la existencia de un campo eléctrico, del que su circulación por un camino arbitrario cerrado es igual a menos la derivada temporal del flujo magnético en cualquier superficie limitada por el camino cerrado.
El signo negativo explica que el sentido de la corriente inducida es tal que su flujo se opone a la causa que lo produce, compensando así la variación de flujo magnético (Ley de Lenz).
La forma diferencial de esta ecuación es:
Esta ecuación relaciona los campos eléctrico y magnético, pero tiene también muchas otras aplicaciones prácticas. Esta ecuación describe cómo los motores eléctricos y los generadores eléctricosfuncionan. Más precisamente, demuestra que un voltaje puede ser generado variando el flujo magnético que atraviesa una superficie dada.
[editar]Ley de Ampère generalizada
Ampère formuló una relación para un campo magnético inmóvil y una corriente eléctrica que no varía en el tiempo. La ley de Ampère nos dice que la circulación en un campo magnético ( ) a lo largo de una curva cerrada C es igual a la densidad de corriente (
) a lo largo de una curva cerrada C es igual a la densidad de corriente ( ) sobre la superficie encerrada en la curva C, matemáticamente así:5
) sobre la superficie encerrada en la curva C, matemáticamente así:5
 ) a lo largo de una curva cerrada C es igual a la densidad de corriente (
) a lo largo de una curva cerrada C es igual a la densidad de corriente ( ) sobre la superficie encerrada en la curva C, matemáticamente así:5
) sobre la superficie encerrada en la curva C, matemáticamente así:5donde 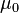 es la permeabilidad magnética en el vacío.
es la permeabilidad magnética en el vacío.
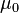 es la permeabilidad magnética en el vacío.
es la permeabilidad magnética en el vacío.Pero cuando esta relación se la considera con campos que sí varían a través del tiempo llega a cálculos erróneos, como el de violar la conservación de la carga.9 Maxwell corrigió esta ecuación para lograr adaptarla a campos no estacionarios y posteriormente pudo ser comprobada experimentalmente. Maxwell reformuló esta ley así:5
En el caso específico estacionario esta relación corresponde a la ley de Ampère, además confirma que un campo eléctrico que varía con el tiempo produce un campo magnético y además es consecuente con el principio de conservación de la carga.9
En forma diferencial, esta ecuación toma la forma:
[editar]En medios materiales
Para el caso de que las cargas estén en medios materiales, y asumiendo que éstos son lineales, homogéneos, isótropos y no dispersivos, podemos encontrar una relación entre los vectoresintensidad e inducción a través de dos parámetros conocidos como permitividad eléctrica y la permeabilidad magnética:10
Pero estos valores también dependen del medio material, por lo que se dice que un medio es lineal cuando la relación entre E/D y B/H es lineal. Si esta relación es lineal, matemáticamente se puede decir que  y μ están representadas por una matriz 3x3. Si un medio es isótropo es porque esta matriz ha podido ser diagonalizada y consecuentemente es equivalente a una función
y μ están representadas por una matriz 3x3. Si un medio es isótropo es porque esta matriz ha podido ser diagonalizada y consecuentemente es equivalente a una función  ; si en esta diagonal uno de los elementos es diferente al otro se dice que es un medio anisótropo. Estos elementos también son llamados constantes dieléctricas y, cuando estas constantes no dependen de su posición, el medio es homogéneo.11
; si en esta diagonal uno de los elementos es diferente al otro se dice que es un medio anisótropo. Estos elementos también son llamados constantes dieléctricas y, cuando estas constantes no dependen de su posición, el medio es homogéneo.11
 y μ están representadas por una matriz 3x3. Si un medio es isótropo es porque esta matriz ha podido ser diagonalizada y consecuentemente es equivalente a una función
y μ están representadas por una matriz 3x3. Si un medio es isótropo es porque esta matriz ha podido ser diagonalizada y consecuentemente es equivalente a una función  ; si en esta diagonal uno de los elementos es diferente al otro se dice que es un medio anisótropo. Estos elementos también son llamados constantes dieléctricas y, cuando estas constantes no dependen de su posición, el medio es homogéneo.11
; si en esta diagonal uno de los elementos es diferente al otro se dice que es un medio anisótropo. Estos elementos también son llamados constantes dieléctricas y, cuando estas constantes no dependen de su posición, el medio es homogéneo.11Los valores de  y μ en medios lineales no dependen de las intensidades del campo. Por otro lado, la permitividad y la permeabilidad son escalares cuando las cargas están en medios homogéneos e isótropos. Los medios heterogéneos e isótropos dependen de las coordenadas de cada punto por lo que los valores, escalares, van a depender de la posición. Los medios anisótropos son tensores.10Finalmente, en el vacío tanto
y μ en medios lineales no dependen de las intensidades del campo. Por otro lado, la permitividad y la permeabilidad son escalares cuando las cargas están en medios homogéneos e isótropos. Los medios heterogéneos e isótropos dependen de las coordenadas de cada punto por lo que los valores, escalares, van a depender de la posición. Los medios anisótropos son tensores.10Finalmente, en el vacío tanto  como
como  son cero porque suponemos que no hay fuentes.
son cero porque suponemos que no hay fuentes.
 y μ en medios lineales no dependen de las intensidades del campo. Por otro lado, la permitividad y la permeabilidad son escalares cuando las cargas están en medios homogéneos e isótropos. Los medios heterogéneos e isótropos dependen de las coordenadas de cada punto por lo que los valores, escalares, van a depender de la posición. Los medios anisótropos son tensores.10Finalmente, en el vacío tanto
y μ en medios lineales no dependen de las intensidades del campo. Por otro lado, la permitividad y la permeabilidad son escalares cuando las cargas están en medios homogéneos e isótropos. Los medios heterogéneos e isótropos dependen de las coordenadas de cada punto por lo que los valores, escalares, van a depender de la posición. Los medios anisótropos son tensores.10Finalmente, en el vacío tanto  como
como  son cero porque suponemos que no hay fuentes.
son cero porque suponemos que no hay fuentes.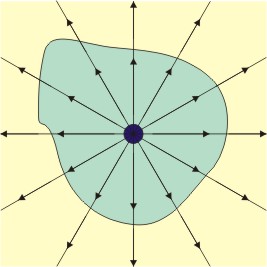


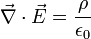




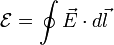
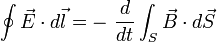




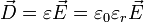

No hay comentarios:
Publicar un comentario